Merkle trees are a fundamental part of what makes blockchains vibrate. Although it is certainly theoretically possible to make a blockchain without Merkle trees, simply by creating giant block headers which directly contain each transaction, this poses major scope of scalability which undoubtedly puts the ability to use blockchains without confidence out of the reach of all the most powerful long-term computers. Thanks to Merkle trees, it is possible to build Ethereum nodes that operate on all large computers and computers large and small smart phones, and even the internet devices of objects such as those that will be produced by Slock.it. So how exactly these Merkle trees work, and what value do they provide, both now and in the future?
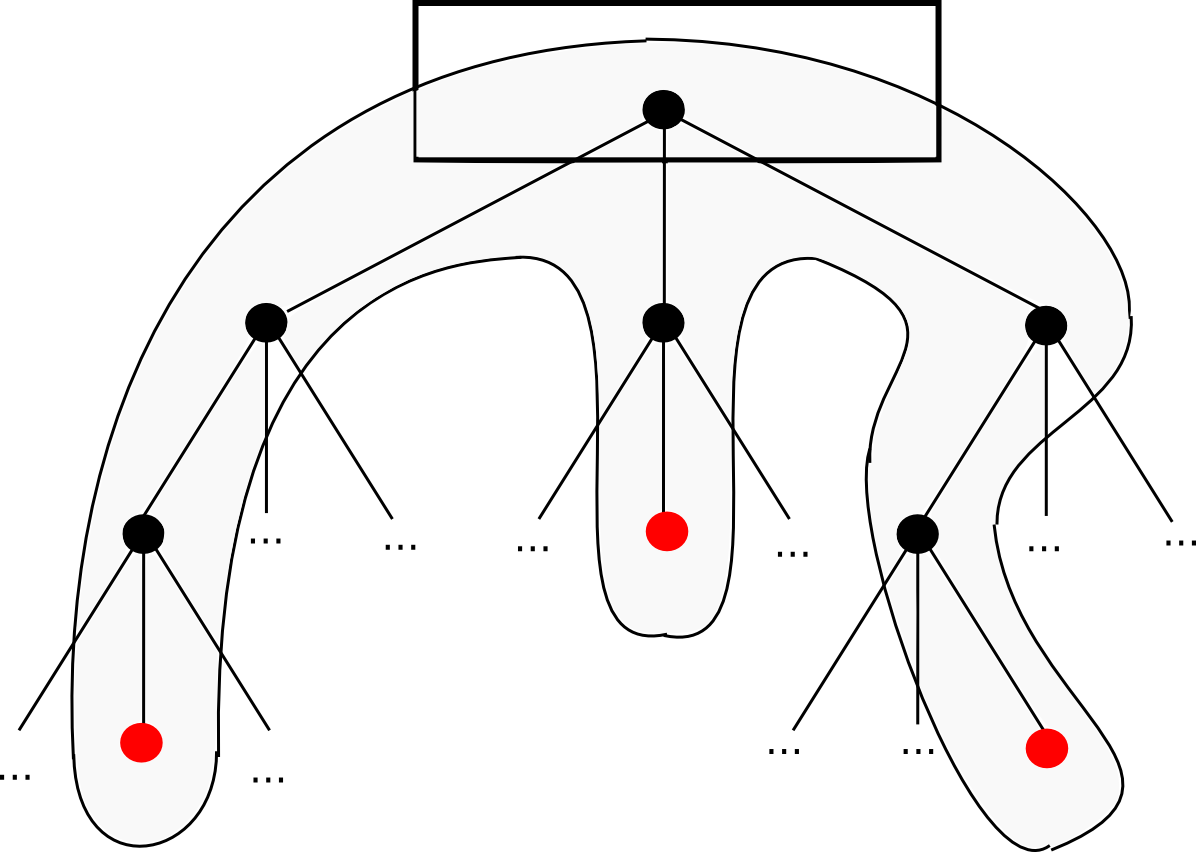
First, the basics. A Merkle tree, in the most general sense, is a means of chopping a large number of “pieces” of data together, which is based on the division of the pieces in buckets, where each bucket contains only a few pieces, then taking the hatch of each bucket and repeating the same process, continuing to do it until the total number of hashs becomes one: root chip.
The most common and simplest shape of the Merkle tree is the Mekle binary tree, where a bucket is always made up of two adjacent pieces or hatches; It can be represented as follows:
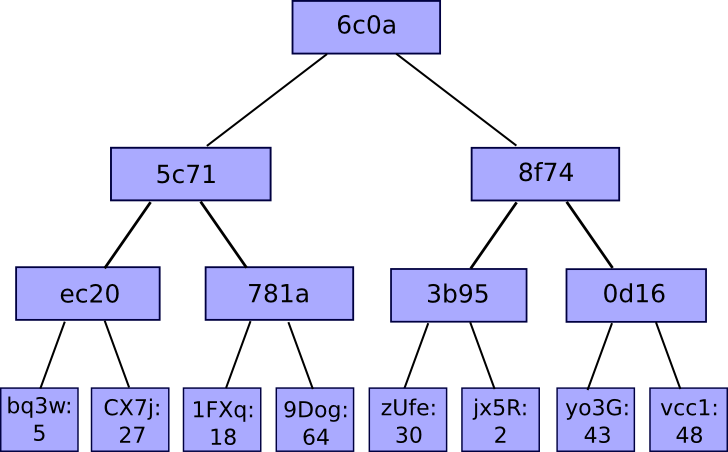
So what is the advantage of this strange type of hash algorithm? Why not just crushed all the pieces together in a single large piece and use a regular hash algorithm on this subject? The answer is that it allows a neat mechanism called Merkle Proomes:
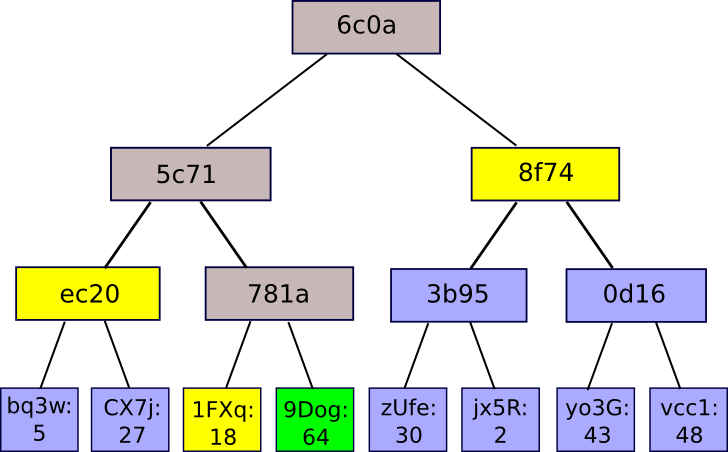
A Merkle test consists of a piece, the roasted hash of the tree and the “branch” composed of all the hashs that go up along the path of the piece at the root. Someone who read the proof can verify that the hash, at least for this branch, will coherent along the tree, and therefore that the given piece is really to this position in the tree. The application is simple: suppose that there is a large database, and that the whole content of the database is stored in a Merkle tree where the root of the Merkle tree is known and reliable (for example, it has been signed digital by sufficient confidence parts, or there is a lot of work proofs). Then, a user who wants to do a key value search on the database (for example. “Tell me the object in position 85273”) can request Merkle proof, and when receiving the proof, check that it is correct, and therefore the value received received is actually In position 85273 in the database with this particular root. It allows a mechanism to authenticate a little amount of data, such as hash, to extend to also authenticate big Potentially unlimited databases.
Merkle Proods in Bitcoin
The original application of Merkle evidence was in Bitcoin, as described and created by Satoshi Nakamoto in 2009. The Bitcoin blockchain uses Merkle evidence in order to store transactions in each block:
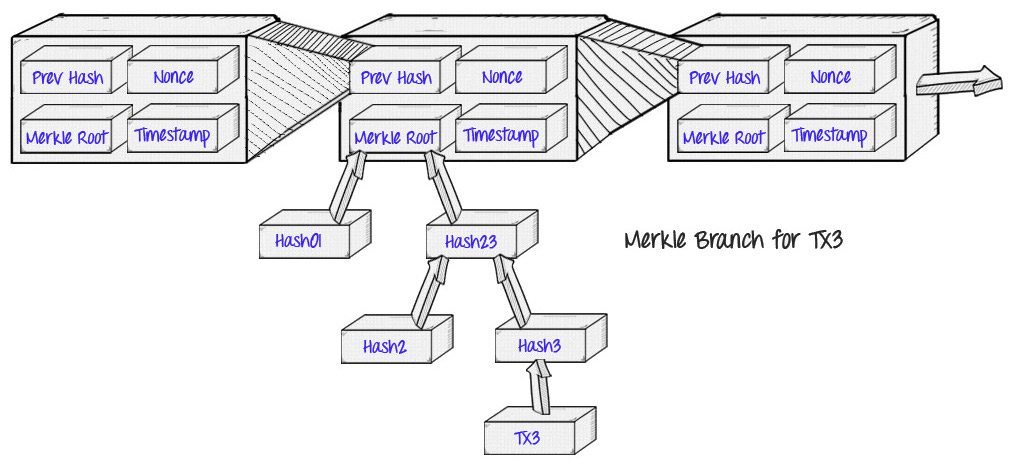
The advantage that this provides is the concept that Satoshi has described as a “simplified verification of payments”: instead of downloading each transaction and each block, a “light customer” can only download the chain of Blocking headbands80 bytes of data for each block which contain only five things:
- A hash of the previous header
- A horoditing
- A value of mining difficulty
- Proof of work nuncio
- A root chopping for the Merkle tree containing the transactions for this block.
If the light customer wishes to determine the condition of a transaction, he can simply request Merkle proof showing that a particular transaction is in one of the Merkle trees whose root is in a block header for the main chain.
It brings us far enough, but light Bitcoin style customers have their limits. A particular limitation is that, although they can prove the inclusion of transactions, they cannot prove anything on the current state (for example, assets of digital assets, name recordings, the state of financial contracts, etc.). How many bitcoins have you right now? A Light Bitcoin client can use a protocol involving the questioning of several nodes and trusting that at least one of them will inform you of the particular transaction expenses from your addresses, and this will take you far enough for this case of use, but for other more complex applications, that was not enough; The precise nature of the effect of a transaction may depend on the effect of several previous transactions, which themselves depend on previous transactions, and therefore in the end, you will have to authenticate each transaction throughout the chain. To get around this, Ethereum makes the concept of Merkle Tree further.
Merkle Proods in Ethereum
Each block header in Ethereum not only contains a Merkle tree, but but three Trees for three types of objects:
- Transactions
- Received (essentially, data showing the effect of each transaction)
- State
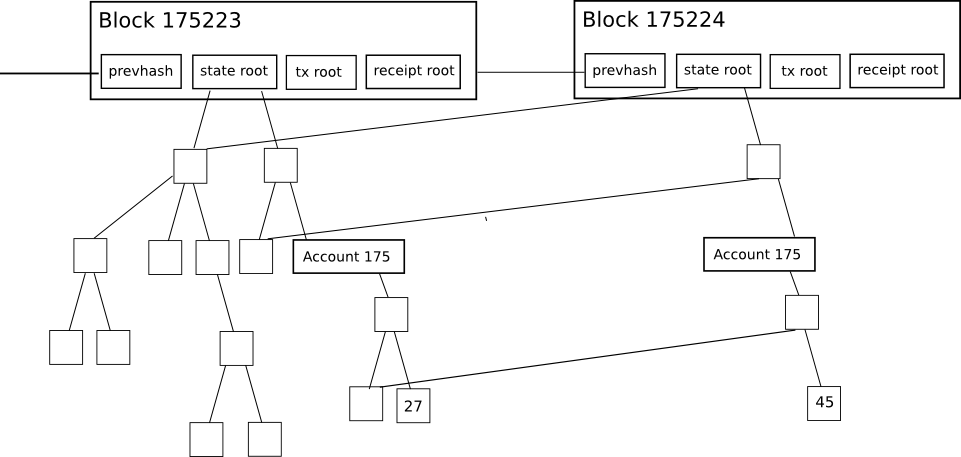
This allows a very advanced light customer protocol that allows mild customers to easily make and obtain verifiable answers to many types of requests:
- Was this transaction included in a particular block?
- Tell me all the cases of an X-type event (for example. A crowdfunding contract achieving its objective) issued by this address in the last 30 days
- What is the current balance of my account?
- Does this account exist?
- Pretend to execute this transaction on this contract. What would be the outing?
The first is managed by the transaction shaft; The third and fourth are managed by the state tree and the second by the reception tree. The first four are quite simple to calculate; The server simply finds the object, recovers the Merkle branch (the list of upgrades of the object at the root of the tree structure) and responds to the light customer with the branch.
The fifth is also managed by the state tree, but the way it is calculated is more complex. Here we must build what we can call a Proof of transition from Merkle’s state. Essentially, it is proof that makes the complaint “if you perform the transaction T On the state with root SThe result will be a state with root S ‘with the newspaper L and outing O“(” Output “exists as a concept in Ethereum because each transaction is a function call; it is not theoretically necessary).
To calculate the proof, the server locally creates a false block, defines the state on S and pretends to be a light customer when applying the transaction. In other words, if the process of applying the transaction requires that the customer determine the balance of an account, the light customer makes a balance request. If the light customer must check a particular element in storing a particular contract, the light customer makes a question for this, etc. The server “responds” to all its own requests properly, but continues to follow all the data it returns. The server then sends the customer the combined data of all these requests as proof. The customer then undertakes exactly the same procedure, but Using the evidence provided as a database; If his result is the same as the server claims, the customer accepts the evidence.
Patricia
It was mentioned above that the simplest type of Merkle tree is the binary merkle tree; However, the trees used in Ethereum are more complex – it is the “Merkle Patricia Tree” that you hear about in our documentation. This article will not fall into the detailed specification; it’s better done by This item And this oneAlthough I will discuss the basic reasoning.
Binary Merkle trees are very good data structures for the authentication of information in a “list” format; Essentially, a series of songs one after the other. For transaction trees, they are also good because it does not matter the time it takes to to modify A tree once it is created, because the tree is created once then solid forever frozen.
For the state tree, however, the situation is more complex. The state of Ethereum consists essentially of a key value card, where the keys are addresses and the values are statements of account, listing the balance, the nonce, the code and storage for each account (where storage is itself a tree). For example, the state of Genesis de Morden Testnet looks like:
{
"0000000000000000000000000000000000000001": {
"balance": "1"
},
"0000000000000000000000000000000000000002": {
"balance": "1"
},
"0000000000000000000000000000000000000003": {
"balance": "1"
},
"0000000000000000000000000000000000000004": {
"balance": "1"
},
"102e61f5d8f9bc71d0ad4a084df4e65e05ce0e1c": {
"balance": "1606938044258990275541962092341162602522202993782792835301376"
}
}
Unlike transactions history, however, the State must be frequently updated: the balance and nonce of accounts are often modified, and moreover, new accounts are frequently inserted and storage keys are frequently inserted and deleted. What is therefore desired is a data structure where we can quickly calculate the new tree root after insertion, update the editing or delete the operation, without recomposing the entire tree structure. There are also two highly desirable secondary properties:
- The depth of the tree is delimited, even given an attacker who deliberately concludes transactions to make the tree as deep as possible. Otherwise, an attacker could make an attack of denial of service by manipulating the tree to be so deep that each individual update becomes extremely slow.
- The root root depends only on the data, not on the order in which the updates are carried out. Updates in a different order and even recompose the tree from zero should not change the root.
THE PatriciaIn simple terms, may be the closest that we can manage to achieve all these properties simultaneously. The simplest explanation of how it works is that the key under which a stored value is coded in the “path” that you need to eliminate the tree. Each node has 16 children, so the path is determined by hexagonal coding: for example, the key dog Hex coded is 6 4 6 15 6 7You would therefore start with the root, descend the 6th child, then the fourth, and so on until you reach the end. In practice, there are some additional optimizations that we can do to make the process much more effective when the tree is sparse, but this is the basic principle. Both items mentioned above Describe all more detail features.




