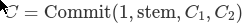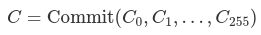A Verkle tree is an engagement system that works similarly to a Merkle tree, but with much smaller witnesses. It works by replacing hashes in a Merkle tree with vector engagement, making larger branching factors more efficient.
Thanks to Kevaundray Wedderburn for his comments on the post.
Preview
For more details on how Verkle shafts work, see:
The aim of this article is to explain the concrete arrangement of the verkle tree project EIP. It is aimed at client developers who want to implement Verkle trees and are looking for an introduction before diving deeper into EIP.
Verkle trees introduce a number of changes to the tree structure. The most significant changes are:
- a change from 20-byte keys to 32-byte keys (not to be confused with 32-byte addresses, which are a separate change);
- merging account and storage attempts; and finally
- The introduction of verkle sorts itself, which uses vector commits instead of hashes.
As a vector engagement scheme for the Verkle tree, we use Pedersen’s commitments. Pedersen’s commitments are based on elliptic curves. For an introduction to Pedersen commitments and how to use them as polynomial or vector commitments using inner product arguments, see here.
The curve we use is Bandersnatch. This curve was chosen because it is efficient, and also because it will allow the efficient SNARKs of BLS12_381 to reason about the verkle tree in the future. This can be useful for rollups as well as allowing an upgrade where all witnesses can be compressed into a single SNARK once it becomes practical, without requiring an additional pledge update.
The order of the curve/size of the bandersnatch scalar field is p = 13108968793781547619861935127046491459309155893440570251786403306729687672801which is a 253-bit prime number. As a result, we can only safely commit to bitstrings of at most 252 bits, otherwise the field overflows. We chose a branch factor (width) of 256 for the Verkle tree, which means that each commit can contain up to 256 values of 252 bits each (or to be precise, integers of up to p-1). We write this as Validate(v₀, v₁, …, v₂₅₅) commit to the list v length 256.
Arrangement of verkle tree
One of the design goals of the Verkle Tree EIP is to make access to neighboring positions (e.g., storage with almost the same address or neighboring pieces of code) inexpensive. To do this, a key is made up of a stem of 31 bytes and one suffix of one byte for a total of 32 bytes. The key scheme is designed such that “nearby” storage locations are mapped to the same stem and a different suffix. For more details, please see the IEP project.
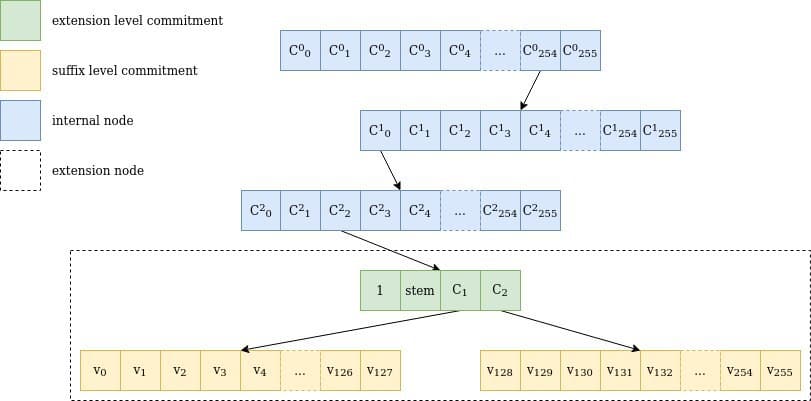
The verkle tree itself is then composed of two types of nodes:
- Extension nodeswhich represent 256 values with the same root but different suffixes
- Internal nodeswhich have up to 256 children, which can be either other internal nodes or extension nodes.
The commitment to an extension node is a commitment to a 4-element vector; the remaining positions will be 0. This is:
C₁ and C₂ are two other commitments that engage on all stem values equal to stem. The reason we need two commits is because the values are 32 bytes long, but we can only store 252 bits per field element. A single commitment would therefore not be enough to store 256 values. So instead, C₁ stores suffix values 0 to 127, and C₂ stores 128 to 255, where the values are split in half in order to accommodate the field size (we’ll get to this later.)
The extension as well as the C₁ and C₂ commitments are called the “extension and suffix tree” (EaS for short).
Figure 1 Depiction of a walk through a verkle tree for the key 0xfe0002abcd..ff04: the path passes through 3 internal nodes of 256 children each (254, 0, 2), an extension node representing abcd..ff and both commitments of the suffix tree, including the value of 04v₄. Note that stem actually matches the first 31 bytes of the key, including the path through the internal nodes.
Commitment to leaf node values
Each extension and suffix tree node contains 256 values. Since a value is 256 bits wide and we can only safely store 252 bits in a field element, four bits would be lost if we simply tried to store a value in a field element.
To get around this problem, we chose to partition the group of 256 values into two groups of 128 values each. Each 32-byte value in a group is split into two 16-byte values. Thus a value vᵢ∈ 𝔹₃₂ is transformed into v⁽ˡᵒʷᵉʳ⁾ᵢ ∈ 𝔹₁₆ and v⁽ᵘᵖᵖᵉʳ⁾ᵢ∈ 𝔹₁₆ such that v⁽ˡᵒʷᵉʳ⁾ ᵢ ++ v⁽ᵘᵖᵖᵉʳ⁾ᵢ= vᵢ.
A “sheet marker” is added to v⁽ˡᵒʷᵉʳ⁾ᵢ, to differentiate between a sheet that was never accessed and a sheet that was overwritten with 0s. No value is ever deleted from a Verkle tree. This is necessary for upcoming state expiration programs. This marker is placed at the 129th bit, i.e. v⁽ˡᵒʷᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ = v⁽ˡᵒʷᵉʳ⁾ᵢ + 2¹²⁸ if vᵢ has already been accessed, and v⁽ˡᵒʷ ᵉʳ ᵐᵒᵈⁱᶠⁱᵉᵈ⁾ᵢ = 0 if vᵢ has no never been consulted.
The two commitments C₁ and C₂ are then defined as
Engagement of extension nodes
The commitment to an extension node is composed of an “extension marker”, which is simply the number 1, the two subtree commitments C₁ and C₂, and the stem of the key leading to this extension node.
Unlike the extension nodes of the Merkle-Patricia tree, which contain only the section of the key that connects the parent internal node to the child internal node, the stem covers the entire key up to that point. This is because Verkle trees are designed with stateless proofs in mind: if a new key is inserted that “splits” the extension in two, the old sibling does not need to be updated, which allows for a smaller proof.
Engagement of internal nodes
Internal nodes have the simplest method of calculating their commitments: the node is seen as a vector of 256 values, which are the (field representation of) the root commitment of each of their 256 subtrees. The commitment for an empty subtree is 0. If the subtree is not empty, then the commitment for the internal node is
where the Cᵢ are the children of the internal node, and 0 if a child is empty.
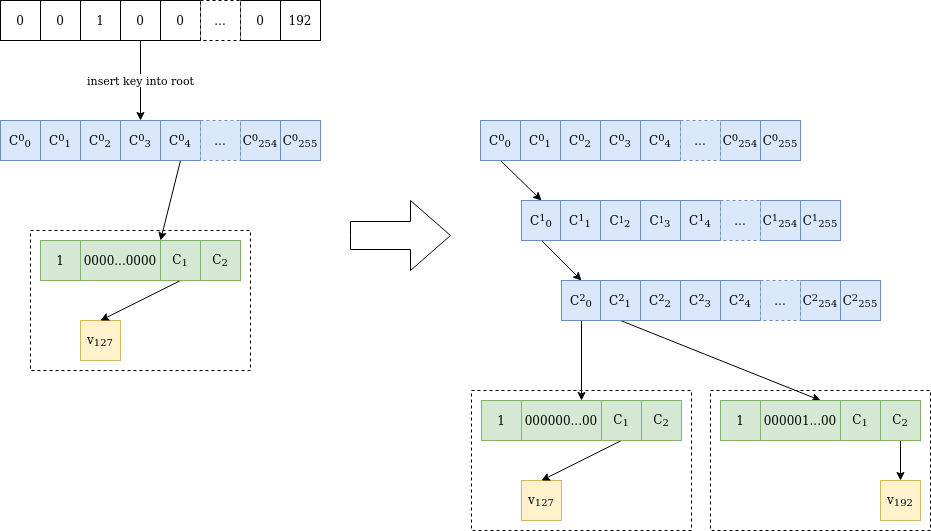
Insertion into the tree
Figure 2 is an illustration of the process of inserting a new value into the tree, which becomes interesting when the stems collide over several initial bytes.
Figure 2 The value v₁₉₂ is inserted at the location 0000010000…0000 in a Verkle tree containing only the value v₁₂₇ at location 0000000000…0000. Since the stems differ at the third byte, two internal nodes are added up to the different byte. Next, another “extension and suffix” tree is inserted, with a full 31 byte stem. The initial node is intact and C²₀ has the same value as C⁰₀ before insertion.
Shallower trees, smaller events
The Verkle tree structure allows for shallower trees, which reduces the amount of data stored. But its real power comes from its ability to produce smaller pieces of evidence, i.e. witnesses. This will be explained in the next article.